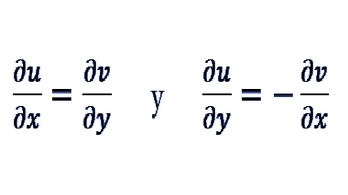
Esta asignatura proporciona los fundamentos y técnicas esenciales para el desarrollo de la teoría de la integración de funciones reales de variable real, ofreciendo las herramientas necesarias para modelar matemáticamente problemas que involucren situaciones de acumulación o cálculo de promedios.
- Profesor: Ángel Gabriel Estrella González
Teoría de la medida e integración
- Profesor: Eric José Ávila Vales
El álgebra lineal es uno de los pilares de las matemáticas, que se encarga de estudiar conceptos tales como vectores, matrices, sistemas de ecuaciones lineales, entre otros. Es una asignatura que es indispensable en la aplicación de las matemáticas, tanto en el ámbito científico como en las más diversas aplicaciones. Su importancia ha venido en aumento debido al uso de computadores de alta velocidad, cálculos a gran escala e incluso está involucrada en decisiones de índole administrativa basadas en modelos de programación lineal.
- Profesor: Javier Arturo Díaz Vargas
Este curso pretende preparar al estudiante para el nivel de abstracción y madurez matemática requeridos en Análisis Matemático y constituir una transición entre los cursos de cálculo previamente estudiados y Análisis.
El curso comienza con un estudio de la topología usual en espacios euclidianos que resulta ser fundamental para tratar con el nivel y profundidad adecuados los temas subsiguientes. Se caracterizan y analizan tres grandes temas de la topología como son la compacidad, la conexidad y la continuidad.
En este curso se estudian también los enunciados y demostraciones de los teoremas del cálculo de funciones de varias variables que resultan ser fundamentales para construir los cimientos de diversas áreas de la matemática, como por ejemplo en geometría diferencial, sistemas dinámicos, ecuaciones diferenciales y otras donde la diferenciación e integración de funciones de varias variables son prerrequisitos tanto por los conocimientos y técnicas empleadas como por la abstracción y madurez matemática adquiridas durante su estudio.
Se estudia la diferenciación e integración en espacios euclidianos, cubriendo los teoremas del valor medio, de la función inversa y de la función implícita, el contenido y la medida cero, las funciones integrables, el teorema de Fubini y el teorema del cambio de variables en integrales múltiples. De esta manera se pretende que el estudiante complete su formación matemática en algunos temas fundamentales del cálculo de varias variables que había aprendido a utilizar en sus cursos previos pero que no había demostrado, avanzando de esa manera en el desarrollo de sus conocimientos y habilidades matemáticas de análisis y síntesis, lógica e intuición, así como también en sus capacidades de abstracción y formalidad matemática.
- Profesor: Lucía Belén Gamboa Salazar
Análisis Numérico es la disciplina intermediaria entre las llamadas matemáticas básicas y la aplicación concreta de los conceptos en otras áreas del conocimiento, estableciendo así un puente fundamental entre las teorías matemáticas y el desarrollo tecnológico. En ella el estudiante plantea, analiza y valora soluciones aproximadas a diversos problemas matemáticos con apoyo computacional.
- Profesor: Ricardo Legarda Sáenz